Executive summary
The debate around funding student loans has largely focused on what share of student loans will be repaid, and what share of the cost will need to be picked up by the taxpayer. Much less attention has been paid to the government cost of financing student loans that do get repaid. In this report, we investigate how the cost of student loans including these financing costs has changed as a result of increases in government borrowing costs over the past two years.
Key findings
1. The cost of government borrowing as measured by the 15-year gilt yield has risen from 1.2% to 4.0% over the past two years. Relative to expected RPI inflation, this is a 3 percentage point increase. As the interest rate on student loans is now the rate of RPI inflation, this means that the government can expect to pay 1.6 percentage points more in interest on its debt than the interest rate it charges on student loans. Two years ago, just before the most recent student loans reform, it could expect to pay 1.4 percentage points less than the rate of RPI inflation.
2. This increase in government borrowing costs translates to an increase in the expected cost of student loans including financing costs of more than £10 billion per year. With borrowing costs as at the end of 2021, the government could have expected to earn a total net profit of £3.2 billion on student loans to the 2023 university entry cohort, arising from the positive spread between the interest it charged on student loans and the interest it paid on its debt. With today’s borrowing costs, this interest rate spread is negative, and the government can expect to make a loss of £7.3 billion.
3. Concerningly, this extra cost is not reflected in either of the government’s official measures of the cost of student loans. The ONS measure does not take the cost of government borrowing into account at all. The DfE measure that underlies the so-called RAB charge uses a backward-looking measure of borrowing costs, which does not yet capture the sharp rise in gilt yields over the last two years.
1. Introduction
The government’s total up-front outlay on student loans in England was around £20 billion in 2022–23 and is forecast to rise to £24 billion by 2027–28. The debate around funding this outlay has largely been framed around what share graduates will repay through student loan repayments, and what share of the cost will need to be picked up by the taxpayer. Much less attention has been paid to the government cost of financing loans that do get repaid.
If the government can borrow at a lower rate of interest than the interest it charges on student loans, then borrowing to lend money to a student who goes on to repay the loan in full will be a profitable transaction for the government (because the interest it pays on its extra borrowing is more than offset by the interest it receives from the student). When the opposite is true, the transaction is loss-making: it becomes costly for the government to provide student loans even to those students who go on to repay them in full, because the interest costs on the government’s borrowing exceed the interest payments received from the student.
In recent years, the government’s borrowing costs have always been lower than the interest rates it charged on student loans. This is now expected to change. Yields on gilts (government bonds) have risen substantially over the past two years and are now higher than expected RPI (Retail Prices Index) inflation, which will determine the interest rate on newly issued student loans. As a result, as well as making a loss on the loans that are not repaid, the government can now also expect to make a loss on the loans that are.
Worryingly, this extra cost is not reflected in the government’s official measures of the cost of student loans. The true additional taxpayer cost due to the recent rise in government borrowing costs is likely around £10 billion per year. The exact number will depend on graduates’ future earnings and future RPI inflation, which governs student loan interest rates; predictions for either of these are highly uncertain. What is certain, however, is that funding student loans has become substantially more expensive for the government over the past two years – and official measures do not reflect that at all.
The remainder of this report is structured as follows. Section 2 compares interest charged on student loans and interest the government pays to finance them – in late 2021 and now. Section 3 discusses how these changes affect the long-run cost of financing student loans, and Section 4 compares these costs with official measures of the cost of student loans. Section 5 draws out some policy implications of our findings.
2. Changing interest rates
One simple way of measuring the government’s cost of financing new borrowing is the annual yield on 15-year gilts, where 15 years is roughly the average time to maturity of outstanding gilts. This yield was just 1.2% at the end of 2021. Over the same 15-year period, RPI inflation was projected by the Office for Budget Responsibility (OBR) to average 2.6%. Expressed relative to projected RPI inflation over the 15-year term, therefore, the gilt yield was negative, at RPI inflation minus 1.4 percentage points (in the usual shorthand, RPI – 1.4%).1 In other words, holding the loan value constant in RPI real terms, financial market participants were willing to pay the government roughly 1.4% of the loan value every year for the privilege of lending it money.2
At the same time, students were charged interest on their loans at a rate between the rate of RPI inflation and the rate of RPI inflation plus 3 percentage points (between RPI and RPI + 3%), depending on their earnings.3 This meant that at the end of 2021, the government could expect to make a profit on the loans of graduates who would eventually pay them off in full, arising from the positive spread between its cost of borrowing (roughly RPI – 1.4%) and the interest charged on student loans (RPI to RPI + 3%).
Figure 1 shows how radically this situation has changed over the past two years. The yield on 15-year gilts was 4.0% at the end of 2023, so roughly 2.8 percentage points higher than at the end of 2021. The OBR now projects RPI inflation to average 2.4% over the next 15 years. Relative to predicted RPI inflation, the 15-year gilt yield has therefore gone up by 3 percentage points to RPI + 1.6%.4
Figure 1. 15-year gilt yields and OBR forecasts for RPI inflation over the next 15 years
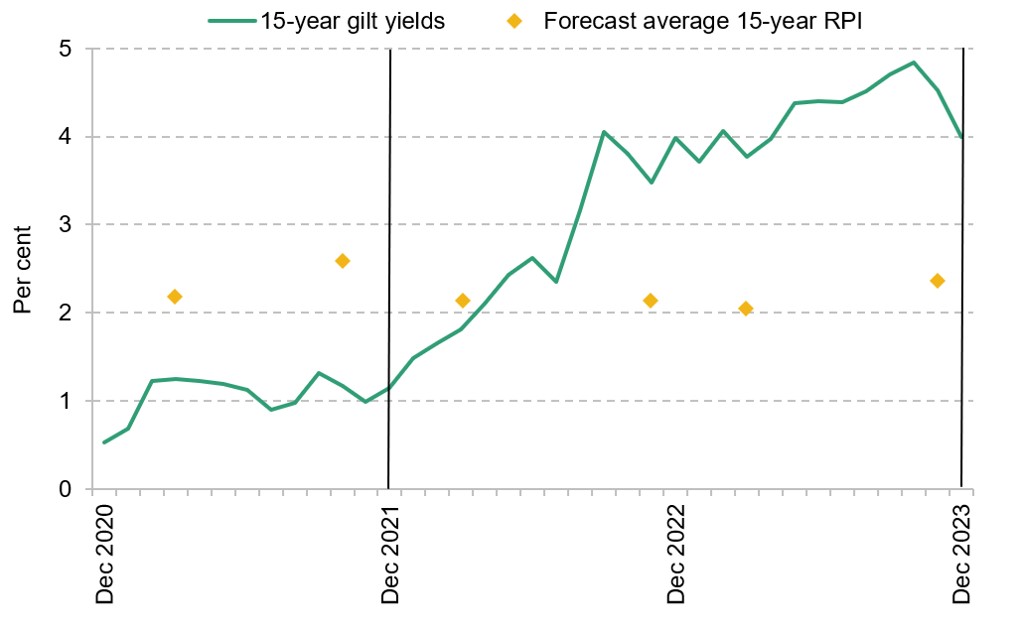
Note: Vertical lines indicate the two points compared throughout the report.
Source: 15-year gilt yields taken from Bank of England historical 15-year month-end spot rates. RPI forecasts taken from OBR Economic and Fiscal Outlooks; the six-year forecast is usually updated twice a year, while the long-run forecast is usually updated every March.
Meanwhile, as a result of the student loans reform that was first announced in February 2022, the interest rate on newly issued undergraduate student loans is now the rate of RPI inflation. The spread between the government’s cost of borrowing (roughly RPI + 1.6%) and the interest rate charged on student loans (RPI) is thus now substantially negative. This means that the government can now expect to lose money on funding even the student loans of those graduates who repay in full.
The sums involved are substantial. In late 2021, the government could expect to gain more than £2,000 a year from high earners early in their career with a typical loan balance of around £50,000 due to the spread between its funding cost and the interest charged on the student loan. If the student loan interest rate had already been at the rate of RPI inflation then, the government could still have expected to gain around £700 per year. Now, it is instead set to lose around £800 a year even on the loans of recent graduates who pay back their loans in full.
3. The long-run cost of loans
The natural way to account for changes in borrowing costs in calculations of the long-run cost of student loans is through the so-called discount rate. The discount rate governs how future receipts are valued relative to up-front outlays; the higher the discount rate, the less valuable is money received in the future relative to today. With a discount rate set equal to the government’s cost of borrowing, the value of future repayments from a given set of student loans is equal to today’s value of a hypothetical portfolio of government bonds that paid out the same amounts as expected loan repayments in any future period.5
If all students paid off their loans in full and the interest rate on student loans were equal to the government’s cost of borrowing, the value of repayments under this measure would be precisely equal to student loan outlays, and the long-run cost would be zero. In reality, not all students pay off their student loans in full, and the interest rate on student loans and the government’s cost of borrowing are not the same. As a result, the long-run cost of loans according to this measure can be positive or negative.
Figure 2 shows estimates of the long-run cost of student loans according to this measure for the 2023 university entry cohort obtained using the IFS student finance calculator, for three different government borrowing costs. First, if government borrowing costs were the same as the interest rate on student loans and thus equal to the rate of RPI inflation, the government would exactly break even on the loans of those who paid off their loans in full. Write-offs on the loans of those who did not repay in full would be expected to cost £2.6 billion in today’s money.
Figure 2. Long-run cost of student loans for the 2023 university entry cohort, including financing costs, at three different costs of government borrowing
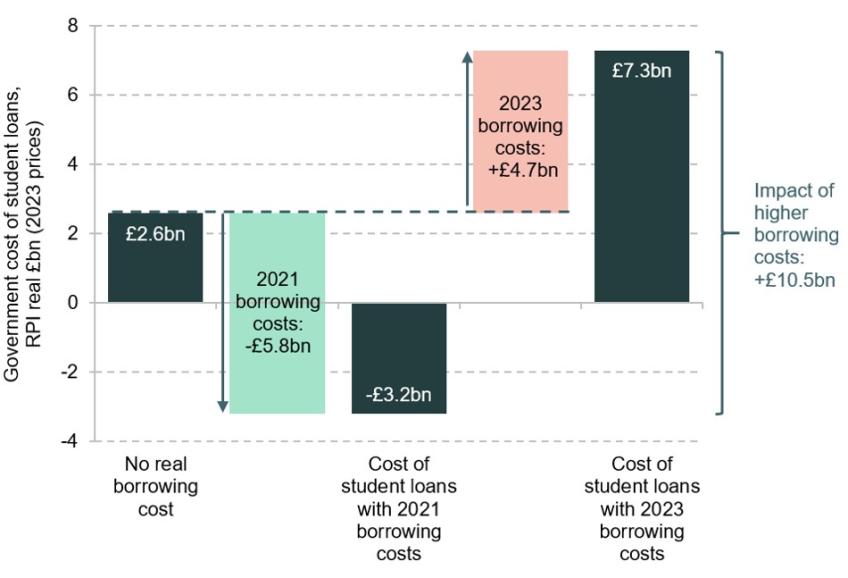
Source: Authors’ calculations using IFS student finance calculator.
Using the actual cost of government borrowing at the end of 2021, as proxied by the 15-year gilt yield, the long-run cost of issuing student loans to the 2023 university entry cohort would have been an expected –£3.2 billion. In other words, with the student loans system as in 2023 and the government cost of funding as at the end of 2021, the government could expect to make a total net profit of more than £3 billion on loans to the 2023 entry cohort, amounting to £6,700 per student. This is because the positive interest rate spread between the expected interest rate on student loans and the government’s cost of borrowing would have outweighed any write-offs from student loans not being paid off in full.
At a discount rate equal to current 15-year gilt yields, the expected total net cost of student loans for the 2023 university entry cohort is £7.3 billion, or over £10 billion more. This means that the government can now expect to make an average loss of £15,200 per student. This is because expected future repayments from the 2023 cohort are much less valuable today, given much higher government borrowing costs. While there are reasonable arguments for considering factors other than borrowing costs at a point in time in setting discount rates for accounting purposes, these numbers clearly illustrate the significance of recent interest rate movements for the cost of funding student loans.
4. How does this compare with official statistics?
Official public finance statistics take a different approach to accounting for the cost of student loans, developed by the Office for National Statistics (ONS). Under this approach, only the share of loans that is not expected to be repaid with interest counts as government spending when loans are issued. Any interest charged on the share expected to be repaid is counted as a receipt in the year in which it is added to the loan balance (actual repayments do not count as receipts).6 Any interest on government borrowing to fund these loans is counted as part of general interest spending, which is a separate spending category in the public finances.
This means that in addition to a spending item when loans are issued reflecting the part of loans that is not expected to be repaid, student loans spending under this approach generally also generates future receipts (interest on the share of student loans expected to be repaid) and future spending (government interest spending). If the student loan interest rate was equal to the government’s cost of borrowing, future interest rate spending on government borrowing to finance the part of student loans expected to be paid back would be just offset by future receipts from interest charged on student loans.
In reality, interest rates on loans can differ from the government’s cost of borrowing. Due to the rise in the government borrowing costs over the past two years, we have gone from a situation where the government could expect future receipts from student loan interest to exceed borrowing costs to finance the part of student loans that is expected to be paid back, to one where borrowing costs are expected be substantially higher than receipts from student loan interest. None of this change is reflected in the public finances at the point when loans are issued, as the share of loans that will be paid off only depends on the interest rate charged on student loans and not on the government’s cost of borrowing.7
A different accounting system is used by the Department for Education (DfE) to calculate the so-called ‘RAB charge’, which – somewhat inaccurately – is commonly cited in policy discussions as a measure of the share of student loans that is not expected to be repaid. To calculate the RAB charge, student loan repayments are discounted at the ‘real financial instrument discount rate’ promulgated by the Treasury. The calculation proceeds in two steps. First, a nominal discount rate is calculated as the backward-looking 10-year rolling average of average-time-to-maturity (roughly 15-year) gilt yields. Then, a prediction for RPI is used to produce a rate relative to RPI inflation.8
While the financial instrument discount rate is thus tied to gilt yields, it largely reflects historical rather than current yields. As gilt yields have increased rapidly over the last two years after a long period of exceptionally low yields, the financial instrument discount rate is now nowhere close to the government’s cost of borrowing. The RAB charge therefore does not reflect actual borrowing costs at the moment, and likely will not for several years to come. In fact, because RPI forecasts are not averaged over 10 years in the same way as nominal gilt yields, the most recent revision of the real financial instrument discount rate has paradoxically been downwards due to higher expected inflation, even though actual expected government borrowing costs have risen substantially in real terms.
All this means that official statistics are likely understating the true cost of the student loans system. The ONS measure focuses only on the share of loans that is not repaid in full and thus misses the spread between government borrowing costs and student loan interest rates, which is now expected to be negative. The RAB charge method fails to account adequately for recent changes in borrowing costs due to the backward-looking approach to choosing the discount rate.
Table 1 summarises how the estimated long-run costs of providing student loans to the 2023 cohort vary under different methodologies. Method 1 shows the estimated cost if future repayments are discounted at the market yield on 15-year gilts from December 2021. This gives a cost of minus £3.2 billion, as described in Section 3. Method 2 repeats the exercise but uses up-to-date 15-year gilt yields. This suggests a cost of £7.3 billion – more than £10 billion higher. Methods 3 and 4 show the substantially lower cost implied by the ONS (£2.6 billion) and RAB charge (£0.4 billion) measures, respectively.
Table 1. Long-run costs of funding undergraduate student loans for the 2023 university entry cohort, different methodologies
| Method | Nominal discount rate | Expressed in terms of (expected) RPI inflation | Long-run cost of student loans (IFS model) |
|---|---|---|---|
| 1. Discounted using yield on 15-year gilts, end of 2021 | 1.2% | RPI – 1.4% | –£3.2bn |
| 2. Discounted using yield on 15-year gilts, end of 2023 | 4.0% | RPI + 1.6% | £7.3bn |
| 3. ONS write-off share | RPI | RPI | £2.6bn |
| 4. RAB charge cost measure (latest) | 1.9% | RPI – 1.3% (pre-reform) RPI – 0.2% (post-reform) | £0.4bn |
Source: Yield data from Bank of England, as of 2 January 2024; IFS student finance calculator.
However, it is worth noting that modelling the cost of student loans generally relies on strong assumptions, and DfE’s own model has long been more pessimistic about graduate earnings and thus student loan repayments than our model. As a consequence, even if we apply a discount rate reflecting the current 15-year gilt yield, our estimate for the long-run cost of student loans for the 2023 entry cohort is only slightly higher than costs implied by official forecasts.
5. Policy implications
As we have long argued, it makes sense for student loan interest rates to be broadly in line with actual long-term government borrowing costs – neither much higher nor much lower. Charging student loan interest significantly below the government’s cost of borrowing amounts to a costly, opaque and oddly-targeted subsidy for student loans. It goes against a fundamental principle behind the current student loans system, which is that graduates who can afford to pay for their own education should do so. Implicit subsidies for student loan interest rates disproportionately benefit higher earners, as they would repay their loans in full even if interest rates were higher (the highest earners benefit somewhat less, as they pay off their loans more quickly). Low-earning graduates who do not pay off their loans in full even at subsidised interest rates never benefit from them.
There is a case for tying the student loan interest rate directly to a measure of the government’s cost of long-term borrowing. An alternative is to set it to the rate of RPI inflation plus a premium to bring it in line with a measure of the government’s cost of long-term borrowing. But the premium would need to be changed again if long-term interest rates relative to RPI inflation changed significantly. (Due to RPI reform, one such change is already expected in 2030.)
Arguments in favour of a higher student loan interest rate need to be weighed against the intuitive appeal of charging no real interest on student loans. As things stand, the government can plausibly claim that no one who started an undergraduate degree since 2023 will need to repay more on their student loan than they borrowed. This may well provide crucial reassurance to some prospective students who might otherwise be deterred from going to university by a fear of taking on large amounts of student debt.
Increasing the interest rate on student loans is also likely to be difficult politically. For one thing, it would lead to higher costs for current students – although it is worth emphasising that these costs would typically not affect their student loan repayments for decades hence. Perhaps more importantly, because of a quirk in student loan accounting in the public finances, a higher interest rate would actually lead to a higher initial cost of student loans recorded in the public finances – even though the long-run taxpayer cost would of course be lower.9













